Программа Расчета Сопротивления Z
Обратный расчет сопротивления термометра или ЭДС термопары. Программа расчета. Также включена программа для расчета сопротивления. Программа для расчета. Сайт электромонтажных работ и электрики, программы, расчеты. Расчёт комплексного сопротивления Z круглого провода переменному току с учётом.
Программа Расчета Сопротивления Zte
Онлайн-калькулятор для расчета сопротивления заземления онлайн.
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида —. Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности. Введем понятие полного сопротивления цепи переменному току - Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных).
Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь. Классификация цепей переменного тока. Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи. Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление. Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения U L (напряжение на индуктивном сопротивлении) и напряжения U R (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°. Полное сопротивление цепи с активным сопротивлением и индуктивностью. А) - схема цепи; б) - сдвиг фаз тока и напряжения; в) - треугольник напряжений; д) - треугольник сопротивлений. Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов U L и U R.
Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор U AB является гипотенузой прямоугольного треугольника. Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов. Напряжение должно равняться силе тока, умноженной на сопротивление. Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z 2) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. (1) Извлекая квадратный корень из обеих частей этого равенства, получим, (2) Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. Полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления.
Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе. Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°. В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления.
Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи. Полное сопротивление цепи с активным сопротивлением и емкостью. А) - схема цепи; б) - треугольник сопротивлений.
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его. Для данного случая: (3) В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи. Полное сопротивление цепи содержащей R, L и C. А) - схема цепи; б) - треугольник сопротивлений. Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений.
Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. (4) Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (X L или X C преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. (5) Или (6) Способ построения треугольника сопротивлений для этого случая изображен на рис. Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления. Полное сопротивление цепи при параллельном соединении активного и реактивного элемента. Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Программа Расчета Сопротивления Zf
Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. А) - параллельное соединение R и L; б) - параллельное соединение R и C. Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL, а полная проводимость равна 1/Z Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. (7) Приводя к общему знаменателю подкоренное выражение, получим: (8) откуда: (9) Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем.
Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению. Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно: (10) Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений. В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7). Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет: (11) Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде: (12) В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. Чтобы соблюдалось условие (13) При соблюдении этого условия полное сопротивление колебательного контура будет равно: (14) где L—индуктивность катушки в Гн; С—емкость конденсатора в Ф; R—активное сопротивление катушки в Ом.
Привет всем форумчанам!! Друзья, выручайте. У нас сейчас практика, и те кто начал ее - безголовые дураки.
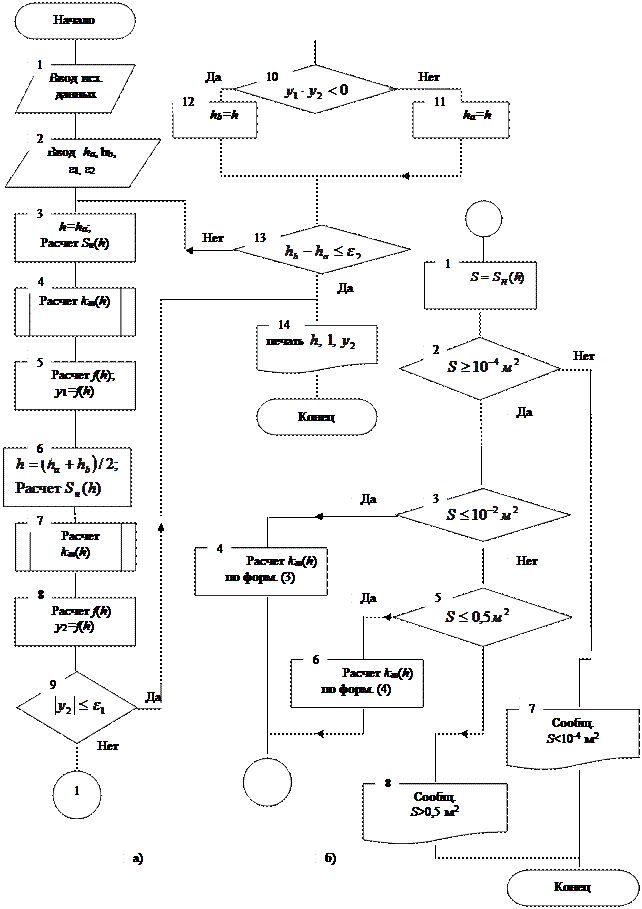
Короче мы сейчас вынуждены практиковаться в C# - и это притом, что у нас опыт в работе на этом языке=0. Мы вообще не работали в нем. А курс С закончили только в прошлом году. Так вот, надо составить несколько задач в C#.
Вот одна из них: Написать программу вычисления сопротивления электрической цепи, состоящей из двух параллельно соединенных сопротивлений. Заранее благодарю, надеюсь на вашу помощь.